Pipedija - tautosaka, gandai, kliedesiai ir jokios tiesos! Durniausia wiki enciklopedija durnapedija!
Dvikampis
Dvikampis - tai tokia matematinė išpera, ir dar tokia išpera, jog matematikai lietuviški net neturi normalaus vertimo ar atitikmens šiai figūrai. Bet, visgi, ji gali egzistuot, tik gal ne neišlenktos erdvės geometrijoje. Tad taip ir gaunasi, jog neparabolinėje geometrijoje gali būti toksai digonas, tokia sferinė figūra kuri turi du kampus. O įsivaizduot tokią figūrą nėra sunku, nes ją aptinkame ir kasdienoje aplinkoje: pavyzdžiui, paimkit kokį vaisių, kaip apelsiną, nulupkite jį, ir gaunam tokias skilteles ir va - visiškai nesunkiai apčiuopiami ir suvokiami dvikampiai ar digonai. Čia panašiai kaip ir sferinėje geometrijoje gali egzistuoti trikampis, kurių visų kampai yra 90°.
Tačiau, net jei ir pats žodis yra suprantamas, ypač su paaiškinimu, matematikai labiau linkę vadint šitą figūrą pusapskritimiu (jeigu 2D), arba sferiniu pleištu (3D).
Įdomiausia šitokio trimačio sferinio pleišto dalis yra tai, kad jis gali būti sudarytas iš trijų plokščių susikertančių paviršių, kurių susikirtimai sudaro tris kraštines, tačiau kampai visvien gaunasi tiktai du. Štai čia yra toksai netiesinės geometrijos paradoksas, nes iš esmės tai reiškia, kad šita figūra skerspjūvyje duoda trikampį, bet kampai visvien gaunasi tiktai du. Ir sukis čia kaip išmanydamas.
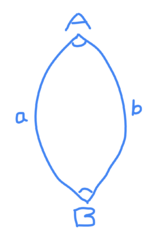
Tiesą sakant, gali dvikampis egzistuoti ne tik trimatėje erdvėje, bet ir dvimatėje, na o bet tačiau gi ta erdvė visvien bus priklausanti neeuklidinei geometrijai, o iš išvaizdos dvimatis trikampis bus panašus į kokį tai lešį ar dar ką nors, ką susigalvosite. Žodžiu, toksai tipiškas atvejis gali būti Rymano paviršiuje nupaišytas daiktas, kuris gali turėti netgi du stačius kampus ir kampų sumą, lygią 180 laipsnių, kaip koksai statusis trikampis, o taip pat vidurinėje dalyje paraleliai einančias kraštines, kaip kokiame kvadrate.
Ne ir dar, galų gale, dvikampis gali egzistuoti ir kaip labai specifinis euklidinės geometrijos atvejis, kur jis bus tiesiog kaip dvi viena su kita sutampančios atkarpos.